DU LERNST HIER...

wie du Python-Bibliotheken numpy und matplotlib im WebTigerPython importieren kannst.

WAS IST NUMPY UND MATPLOTLIB?

numpy ist ein Python-Erweiterungsmodul, welches für die wissenschaftlichen Berechnungen verwendet wird. Da dieses Modul mit C geschrieben ist, werden nummerische Berechnungen mit numpy viel schneller als mit Standard-Python ausgeführt. Ausserdem bereichert nympy Python um mächtige Datenstrukturen für das effiziente Rechnen mit grossen Arrays und Matrizen.
matplotlib wird für die Visualisierung und grafische Darstellung von Daten verwendet.

MUSTERBEISPIELE

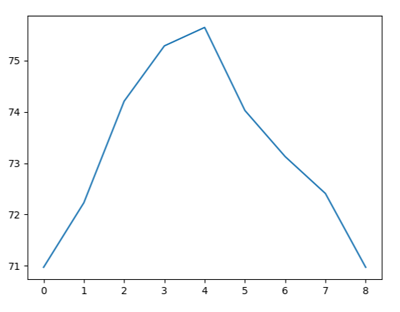
Beispiel 1: Eine Datenreihe grafisch darstellen
Du importierst die Module numpy und matplotlib. Es ist üblich diesen Imports kurze Alias np und plt zu geben, die dann im Programmcode verwendet werden. Die Liste
values konvertiertst du mit np.array() zum numpy array und berechnest die Werte des Arrays v. Mit der Funktion plot() aus dem Modul mathplotlib stellst du das Array im Koordinatensystem dar.

Programm:  [► WebTigerPython]

#Gp16a.py
import numpy as np
import matplotlib.pyplot as plt

values = [20.1, 20.8, 21.9, 22.5, 22.7,21.8, 21.3, 20.9, 20.1]
a = np.array(values)
v = a * 9/5 + 34.789
print(v)
plt.plot(v)
plt.show()

Beispiel 2: Funktionsgraphen
Das Modul numpy unterstützt viele mathematische Funktionen (https://numpy.org/doc/stable/reference/routines.math.html).
Diese kannst du sehr einfach mit matplotlib grafisch darstellen. Dabei wird das passende Koordinatensystem automatisch hinzugefügt.

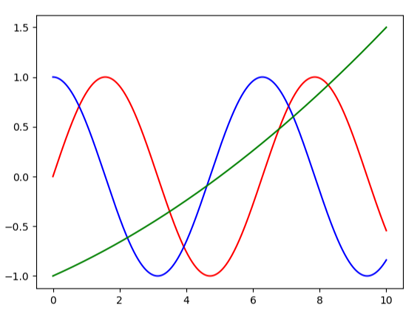
Die Funktion arange(start, stop, step) aus dem Modul numpy liefert ein halboffenes Intervall [start, stop) mit Abstand step, zwischen zwei nacheinander folgenden Werten.
(start gehört dazu, stop nicht). Im Unterschied zur Python-Funktion range(start, stop, step) , die eine Liste mit ganzzahligen Werten liefert, sind bei arange(start, stop, step) auch Dezimalzahlen möglich.
np.arange(0, 10.01, 0.01) liefert also ein Array mit den Zahln 0, 0.1, 0.2, 0.3 ......10.
plt.plot(x, f1, color= "red") stellt für alle Werte des Arrays die Funktionswerte f1(x) mit der roten Farbe im Koordinatensystem dar.

Programm:   [► WebTigerPython]

#Gp16b.py
import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0, 10.01, 0.01)
f1 = np.sin(x)
f2 = np.cos(x)
f3 = 0.01 * x**2 + 0.15 * x - 1
plt.plot(x, f1, color="red")
plt.plot(x, f2, color="blue")
plt.plot(x, f3, color="green")
plt.show()

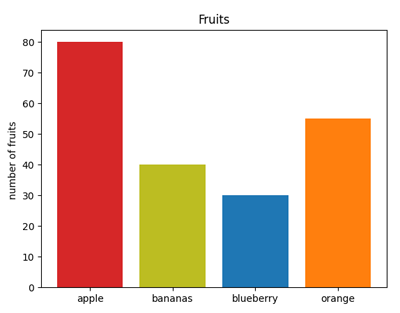
Beispiel 3: Säulendiagramm
Im nächsten Beispiel wird Anzahl Früchte mit einem Farbigen Säulendiagramm dargestellt. Mit set_titel() und set_ylabel() fügst du den Titel und die Beschriftung der y-Achse hinzu.

Programm:   [► WebTigerPython]

#Gp16c.py
import matplotlib.pyplot as plt

fig, fx = plt.subplots()
fruits = ['apple','bananas','blueberry', 'orange']
counts = [80, 40, 30, 55]
bar_colors = ['tab:red','tab:olive','tab:blue','tab:orange']
fx.bar(fruits, counts, color=bar_colors)
fx.set_ylabel('number of fruits ')
fx.set_title('Fruits')
plt.show()

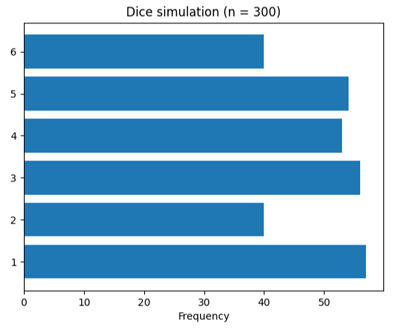
Beispiel 4: Balkendiagramm
Hier verwendest du ein Balkendiagramm, um die Ergebnisse einer Würfelsimulation darzustellen. Du definierts eine Funktion countFrequency(), die 300 zufällige Würfelzahlen erzeugt und die Häufigkeiten, mit welchen die einzelnen Zahlen vorkommen berechnet. Mit einem Balkendiagramm stells du diese Häufigkeiten im Koordinaten system dar.
Lasse das Programm mehrmals laufen und vergrössere die Zahl der Würfe n.

Programm:   [► WebTigerPython]

#Gp16d.py
import matplotlib.pyplot as plt
import numpy as np
from random import randint

def countFrequency():
    global a
    n = 300
    for i in range(n):
        r = randint(1, 6)
        if r == 1:
            a[0] += 1
        elif r == 2:
            a[1] += 1
        elif r == 3:
            a[2] += 1 
        elif r == 4:
            a[3] += 1
        elif r == 5:
            a[4] += 1
        elif r == 6:
            a[5] += 1     

fig, fx = plt.subplots()
diceNumbers = ('1', '2', '3', '4', '5', '6')
a = [0, 0, 0, 0, 0, 0]
y_pos = np.arange(len(diceNumbers))
countFrequency()
frequency = [a[0], a[1], a[2], a[3], a[4], a[5]]
fx.barh(y_pos, frequency, align='center')
fx.set_yticks(y_pos, labels=diceNumbers)
fx.set_xlabel('Frequency')
fx.set_title('Dice simulation (n = 300)')
plt.show()

MERKE DIR...

Mit import numpy und import matplotlib kannst in WebTigerPython mächtige Python-Erweiterungsbibliotheken importieren, die du für wissenschaftliche Berechnung und grafische Darstellung von Zahlenmaterial verwenden kannst.

ZUM SELBST LÖSEN

Stelle die Funktion
f = x³ - 9x
im Bereich -4 < x < 4 grafisch dar.

Die aus der Physik bekannte Funktion
y = ae^-kt sin(ωt + pi/2)
stellt eine gedämpfte harmonische Schwingung dar.
a: Anfangsamplitude
k: Dämpfungskonstante
omega: Kreisfrequenz des ungedämpftes Systems

Die Funktionswerte kannst du mit Hilfe von Funktionen exp() , sin(), pi aus dem Modul np berechnen:

f = a * np.exp(-k * x) * np.sin(omega * x + np.pi/2)

Stelle die Funktion für die Werte
a = 5
k = 0.04
omega = 0.6
im Bereich 0 < x < 100 grafisch dar.